|
|
Eğitim Öğretim İle İlgili Belgeler > Konu Anlatımlı Dersler > Matematik Dersi İle İlgili Konu Anlatımlar
ARİTMETİK DİZİ, DİZİLER, ÖZELLİKLERİ, DİZİLER (MATEMATİK DERSİ İLE İLGİLİ KONU ANLATIMLAR, ÇÖZÜMLÜ ÖRNEKLER, SORULAR)
Ardısık terimlerinin arasındaki farkın sabit oldugu dizilere aritmetik dizi denir.
( n) = (1, 2, 3, 4, ..., n, ...) dizisi bir aritmetik dizidir örnegin, çünkü her ardısık terim arasındaki fark 1dir.
Dikkat edin, farka 1 demedik çünkü bu farkı bulurken iki terim arasındaki farkın mutlak degerini almıyoruz, herhangi bir terimden kendinden bir önce gelen terimi çıkartıyoruz.
Adına da ortak fark diyoruz. Ortak farkı, dyle göstermek adet olmus, biz de öyle yapacagız.
(n) = (1, 2, 3, 4, ..., n, ...) aritmetik dizisinde
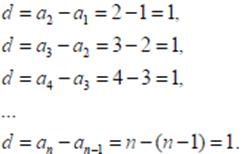
Benzer sekilde (2n + 7) = (9, 11, 13, ..., 2n + 7, ...) dizisi de aritmetik dizidir. Bunda ortak fark 2dir.
(3− 4n) = (−1,− 5,− 9, ..., 3− 4n, ...) dizisi de bir aritmetik dizidir. Ortak farkı 4tür.
Tahmin edilecegi üzere (an) (5) (5, 5, 5, ..., 5, ...) n a = = gibi sabit diziler de aritmetik dizidir, ortak farkı 0dır.
Genel olarak, (an + b) aritmetik dizisinin ortak farkı adır diyebiliriz, neden oldugunu siz düsünün.
Soru 1.
![]()
dizisi bir aritmetik dizi midir? Öyleyse, ortak farkı kaçtır?
Çözüm: Eger aritmetik diziyse ardısık terimleri arasındaki fark sabit bir sayı olmalı, devamlı degismemeli.
Yanılmamak için 2nci ve 1inci terimin arasındaki farkla, 4üncü ve 3üncü terimler arasındaki farkları kıyaslamak yerine (n + 1)inci ve nninci terimler arasındaki farka bakalım:
![]()
yani sabit oldugundan dizi aritmetik olup, ortak farkı 3dür.
Soru 2.
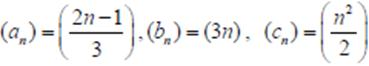
dizilerinden hangisi veya hangileri bir aritmetik dizidir?
Çözüm: a ve b birer reel sayı olmak üzere cn = an + b genel terimine sahip her (cn ) dizisi aritmetiktir.
![]() farkını
hesaplayanlar cevabın her zaman a çıkacagını göreceklerdir. Bundan
farkını
hesaplayanlar cevabın her zaman a çıkacagını göreceklerdir. Bundan
dolayı ![]() aritmetik
dizidir.
aritmetik
dizidir.
Hatta ortak farklar da sırasıyla
![]()
Fakat (cn) aritmetik dizi degildir. Çünkü a2 a1 ile a3 a2 farkları esit degildir. İnanmayan hesaplasın,görsün.
Bir aritmetik dizinin herhangi bir terimini bulmak:
Aritmetik dizilerin herhangi iki terimi veya herhangi bir terimiyle ortak farkı biliniyorsa, dizinin tüm terimleri bulunabilir.
Eni sonu iki bagımsız bilgiye ihtiyaç vardır. Çünkü terimler arasında asagıdaki gibi bir iliski vardır:
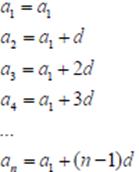
Yukardan da görüldügü gibi ilk terim ve ortak fark bilgisiyle bulunamayacak terim yok. Hatta birkaç oynamayla baska iliskiler de bulmak mümkün.
Örnegin,
![]() .
.
Yani iki terim arasındaki fark, bu terimlerin indisleri farkı kadar d.
Anlayacagınız söyle bir esitlikten bahsedebiliriz:
![]()
Bu esitligi, çözümlerde sıkça kullanacagız.
Lütfen unutmayın. Ama (bilgi yelpazesi.net) unutmamak için ezberlemeye çalısmayın, neden böyle olduguna bir kez daha kafa yorun.
Soru 3. lk terimi a1 = 3, ortak farkı d = 2 olan bir aritmetik dizinin besinci terimini ve genel terimini bulunuz.
Çözüm: ![]() soruluyor.
Bunların formüllerini yukarda çıkarmıstık
soruluyor.
Bunların formüllerini yukarda çıkarmıstık
![]()
ve
![]()
Besinci terimi, genel terimi bulduktan sonra nye 5 vererek de bulabilirdik.
Soru 4. lk terimi a1 = -2, ortak farkı
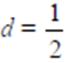
Olan bir aritmetik dizinin 12nci terimini bulunuz.
Çözüm:
![]()
Soru 5. lk terimi 2, ortak farkı
![]()
olan bir aritmetik dizinin kaçıncı terimi 3tür?
Çözüm: Diyelim ki tninci terimi 3. O halde
![]()
esitligi çözülürse t = 5 bulunur.
Soru 6. Üçüncü terimi a3 = 1, ortak farkı
![]()
olan bir aritmetik dizinin kaçıncı terimi 5tir?
Çözüm: Yine tninci terim olsun. O halde
![]()
esitligi çözülürse t = 15 bulunur.
Soru 7. lk terimi 3, son terimi 91 ve ortak farkı -4 olan sonlu aritmetik dizinin terim sayısı kaçtır?
Çözüm: Bunu sayılar dersinde ögrendigimiz terim sayısı formülünden de yapabiliriz ama oradan yapmayacagız.
Dizimiz n terimli olsun.
O halde ![]() olur.
olur.
![]()
denklemi çözülürse n = 23 bulunur.
|
|
Soru 8. 14 ve 50 arasına, bu sayılarla birlikte aritmetik dizi olusturacak biçimde 11 terim daha yerlestirilirse bu dizinin 9uncu terimi kaç olur?
Çözüm: 2 terim hali hazırda vardı, 11 terim daha geldi, etti 13 terim. O halde son durumda a1 =14 ve a13 = 50 oldu.
![]()
esitliginden 12d = 36 yani d = 13 bulunur.
Simdi sıra 9uncu terimde
![]()
Soru 9. 8 ile 50 sayıları arasına, bu sayılarla aritmetik dizi olusturacak sekilde 62 terim yerlestirilirse, bu dizinin 19uncu terimi kaç olur?
Çözüm: Var olan 2 terime 62 terim geldi ve dizimiz 64 terimli oldu. Su halde
![]()
![]()
esitliginden
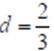
bulunur.
Şimdi 19uncu terimi hesaplayalım:
![]()
Soru 10. Bir aritmetik dizide
![]()
İse a19 kaçtır?
Çözüm: 26 12 a − a = (26 −12)d =14d oldugunu biliyoruz.
Degerleri yerlerine yazarak dyi bulalım:
79 9 = 70 = 14d esitliginden d = 5 bulunur.
O halde
![]()
olur.
Simdi burada biraz soluklanalım. Buna degecek çünkü sonunda yukardaki soruyu 1 saniyede çözmeyi ögrenecegiz.
Aritmetik dizinin en karakteristik özelliklerinden biri de dizinin herhangi terimin, kendine esit uzaklıkta bulunan terimlerin aritmetik ortası oldugudur.
Bunu nerden mi çıkardık?
Dinleyin:
Bir aritmetik diziden herhangi bir terim seçelim, örnegin nninci terim olsun. Simdi de bu terime esit uzaklıkta iki terim daha alalım. Bunlar da örnegin (n p)ninci ve (n + p)ninci terimler olsun.
Kanıtlamak istedigimiz esitlik:
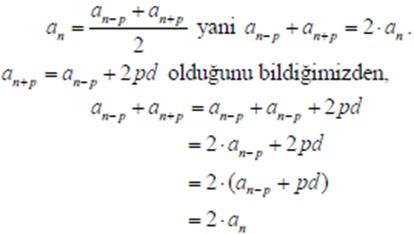
oldugu rahatlıkla görülebilir. İşte bu yüzden bir önceki soruda
![]()
esitligine hemencecik ulasabilirdik.
Soru 11. Besinci terimi 17, 23üncü terimi 47 olan bir aritmetik dizinin 14üncü terimi kaçtır?
Çözüm: 14üncü terimin 5inci ve 23üncü terimlere uzaklıkları esit oldugundan,
![]()
olmalıdır ki buradan a14 = 32 bulunur.
Soru 12. (an) bir aritmetik dizi,
![]()
ise a21 kaçtır?
Çözüm: 16ıncı terimin 11 ve 21inci terimlere uzaklıkları esit oldugundan yine aritmetik ortadan faydalanacagız.
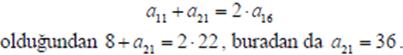
Soru 13. (an) n a bir aritmetik dizi,
![]()
ise a17 kaçtır?
Çözüm
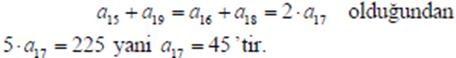
Soru 14. 2, loga 3, 8 sayıları bir aritmetik dizinin ardısık üç terimiyse a kaçtır?
Çözüm: loga 3 = 5 olmalı. O halde
![]()
Soru 15. 5, a, b, c, 13 sayıları bir aritmetik dizinin ardısık bes terimiyse a + b + c toplamı kaçtır?
Çözüm: 5 + 13 = a + c = 2b oldugundan a + c = 18 ve b = 9 olur. O halde cevap 27.
Soru 16.

olan bir aritmetik dizinin genel terimi nedir?
Çözüm:

Genel terim demek nninci terim demek oldugundan ve elimizde 5inci terim oldugundan ikisi arasında bir baglantı (bilgi yelpazesi.net) kuracagız.
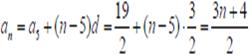
Soru 17.
![]()
olan bir aritmetik dizide a8 kaçtır?
Çözüm:
![]()
2dir.
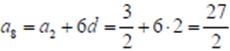
Soru 18. Bir (an) dizisinde
![]()
için
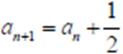
ise a9 kaçtır?
Çözüm:
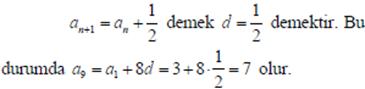
İlk n terimin toplamının bulunması:
Aritmetik dizilerde artıs miktarı aynı oldugundan Sayılar dersinde kanıtladıgımız
![]()
eşitligini kullanabiliriz. Ama kullanmayacagız.
Ona denk baska bir formül çıkartacagız. O daha kullanıslı oldugundan bundan sonra onu kullanacagız.
İlk n terimin toplamını Sn ile gösterecegiz.
![]()
oldugundan, her terimi a1e baglı olarak yazıp, öyle toplayalım bakalım ne çıkıyor

Simdi bu esitlikleri taraf tarafa toplayacagız. Toplam n tane satır olduguna dikkat ediniz.
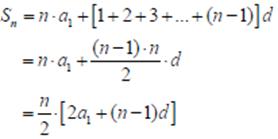
Soru 19. 6 + 11 + 16 + + 116 + 121 toplamı, bir aritmetik dizinin ilk n teriminin toplamı ise bu toplam kaçtır?
Çözüm: Bu ilk soru oldugundan 3 degisik çözüm yolu verelim. İki sayılar dersindeki formülümüzden, ikincisi toplam sembolünden yararlanarak, üçüncüsü de Sn formülünden
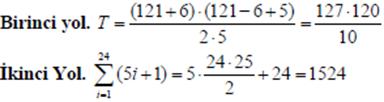
Üçüncü Yol. Bir önceki çözümden dizinin 24 terimli oldugunu ögrendik. Sn formülünde n yerine 24 yazacagız:
![]()
Soru 20. Genel terimi
![]()
olan bir aritmetik dizinin ilk 21 teriminin toplamı kaçtır?
Çözüm: Genel terim belli oldugundan a1 ve dyi biliyoruz demektir, o halde ne duruyoruz?
![]()
Soru 21. Birinci terimi 8, ikinci terimi
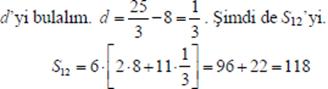
Soru 22. lk terimi
![]()
ve ilk 18 teriminin toplamı 23 olan bir aritmetik dizinin ortak farkı kaçtır?
Çözüm:
![]()
Soru 23. 10 terimli bir aritmetik dizinin terimlerinin toplamı 20, son ve ilk terimlerinin farkı 8 ise bu aritmetik dizinin genel terimini bulunuz.
Çözüm: Verilen bilgileri matematik diline bir çevirelim bakalım.
![]()
Genel terimi bulmak için a1 ve dyi bulmalıyız. Verilen ikinci esitlikten bunları bulabiliriz. Simdi dediklerimizi yapmaya baslayalım, sonra da baska bir yol daha gösterelim.

olacagından a10 + a1 = 4tür. Diger yandan a10 a1 = 8 verildiginden a1 = 2 bulunur. Gerisi yukardaki gibi yapılır.
Soru 24. Bir aritmetik dizide ilk n terimin toplamı

ise bu dizinin 8inci terimi kaçtır?
Çözüm: İşte en begendigim soru tarzı bu. Çözümü çok zekice. 8inci terimi söyle bulacagız:
İlk 8 terimin toplamından, ilk 7 terimin toplamını çıkartacagız.
![]()
Soru 25. Bir aritmetik dizide ilk n terimin toplamı
![]()
ise a15 kaçtır?
Çözüm: Bu sefer ilk 15 terim toplamından ilk 14 terim toplamını çıkartacagız.
![]()
Soru 26. Bir aritmetik dizide 42nci terim 101, 30uncu terim 61 ise bu dizinin ilk 71 teriminin toplamı kaçtır?
Çözüm:

Soru 27. Bir aritmetik dizide 29uncu terim 37, 17nci terim 15 ise bu dizide S45 kaçtır?
Çözüm: Bir öncekiyle benzer soru oldugundan çözümü de bir öncekiyle benzer olacak.

Soru 28. Bir öğrenci ilk gün bir kitaptan 10 sayfa okuyor. Diger günler ise bir önceki gün okuduğundan 5 sayfa fazla okuyor. Bu (bilgi yelpazesi.net) öğrenci, onuncu günün sonunda toplam kaç sayfa okumuş olur?
Çözüm: Her gün okuduğu sayfa sayısındaki artıs miktarı sabit oldugundan, ilk günden itibaren her gün okunan sayfa sayıları bir aritmetik dizi olustururlar.
O halde
![]()
kaçtır diye algılamamız lazım soruyu.
![]()
Soru 29. Bir dısbükey besgenin iç açı ölçüleri bir aritmetik dizinin ardısık bes terimini olusturacak sekildeyse, ortanca açının ölçüsü kaç derecedir?
Çözüm:
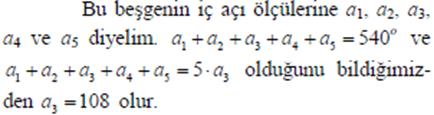
Soru 30. Bir dısbükey besgenin iç açı ölçüleri bir aritmetik dizinin ardısık bes terimini olusturacak sekildedir. En küçük ölçüye sahip açının ölçüsü 800 ise en büyük ölçüye sahip olanın ölçüsü kaç derecedir?
Çözüm: Açı ölçülerini tekrar yukardaki gibi adlandıralım.
Ortanca yani a3 daima 1080 olacagından
ve

|
|
>>>TIKLAYIN<<<
KONU ANLATIMLI DERSLER " SAYFASINA GERİ DÖNMEK İÇİN
>>>TIKLAYIN<<<
MATEMATİK DERSİ İLE İLGİLİ TEST SORULARI SORU BANKASI "
SAYFASINA GEÇMEK İSTERSENİZ
>>>TIKLAYIN<<<
MATEMATİK DERSİ İLE İLGİLİ YAZILI SORULARI "
SAYFASINA GEÇMEK İSTERSENİZ
>>>TIKLAYIN<<<
"EĞİTİM ÖĞRETİM İLE İLGİLİ BELGELER SAYFASINI GÖRMEK İSTERSENİZ
>>>TIKLAYIN<<<
| ||||